
재미있게 읽은 책 <수학자의 생각법> 두 번째 포스팅이다.
책에서 남기고 싶은 문장들과 소감을 번갈아 가며 정리했다.
제4장 기하학의 지름길
콜롬버스는 이 잘못된 계산 덕분에 가야 할 거리의 반밖에 안 되는 바다 한가운데에서 음식과 보급품이 바닥날 수밖에 없는 운명에 처했다. 하지만 다행히도 산살바도르라는 바하마의 작은 섬에 우연히 발을 디디게 되었다. 그는 실수를 깨닫지 못한 채 자신이 동인도 제도에 도착했다고 생각했다. 그리고 그는 그 섬의 주민들을 인도 사람들이라는 뜻의 인디언이라고 불렀다. (164)
콜롬버스가 거리를 잘못 계산해서 인도까지 도달할 수 없는 상태로 항해를 시작했다는 사실을 알 수 있다. 계산의 기본은 어느 단위를 적용하는지 잘 이해하는 것이다. 이 역사의 순간에도 수학이 개입되어 있다.
머리 위에 태양이 올라오는 하지가 되면 시에네의 우물에는 그림자가 생기지 않는다. 반면 알렉산드리아에 세운 기둥에는 북쪽으로 그림자가 생긴다. 기둥의 그림자 길이와 기둥의 길이를 측정한 후 에라토스테네스는 이를 이용하여 같은 비율의 삼각형을 만들고 삼각형 내부의 각도를 측정하였다. 이 정보를 이용하면 지구 둘레상에서 알렉산드리아가 시에네로부터 얼마나 멀리 떨어져 있는지를 알 수 있었기 때문이다. (168)
그림자를 관찰한 결과에서 아이디어를 얻어 시에네와 알렉산드리아의 거리를 측정한 에라토스테네스는 훌륭한 과학자이며 측량사다. 그가 이 거리를 알아야 할 이유가 있지 않았을까. 단순히 호기심만으로 했을까라는 의구심이 든다.
로버트 맥팔레인Robert Macfarlane은 저서 <오래된 길> The Old Ways에서 걷기와 사고 사이의 연관성에 대해 이야기한다. 그는 비트겐슈타인이 어떻게 노르웨이의 시골길을 걸으면서 자신의 연구에서 중요한 돌파구를 발견했는지를 이렇게 묘사한다. "내 안에 새로운 사상을 낳은 것 같다'라고 철학자는 썼다." (191)
산책이나 조깅과 같은 육체적인 활동을 통해 정신적으로 잡념이 사라지는 경험을 자주 한다. 단순히 걷고 뛰는 행동 자체에 집중하게 된다. 조용한 이런 활동 중에 머릿속으로 번뜩이는 아이디어가 떠오르기도 한다. 하나에 집중할 수 있다. 비트겐슈타인의 말처럼 '사상'을 낳는 경지까지 이를 수 있다.
셰퍼드는 1940년대에 쓴 <살아 있는 산>The Living Mountain의 결말에서 울프와 워즈워스 등이 얘기했던 소위 '존재의 순간'이 어떻게 만들어지는지에 대해 썼다. 그는 '존재의 순간은 걸을 때만 만들어진다. 한 시간, 두 시간 걷다 보면 감각이 살아나고 우리의 육체는 투명해진다'라고 말했다. (192)
감각이 살아나고 육체는 투명해진다는 말이 아름답게 들린다. 존재의 순간이 걸을 때에 만들어진다는 말도 감미롭게 들린다. 2025년에는 많이 움직이는 한 해가 되야겠다. 마음이 아름답게 되도록.
수학적 난관에 부딪히면서 느끼는 좌절감 뒤에 그것을 극복해내고 느끼는 희열이 따라온다는 것을 잘 알고 있다. 맥팔레인과 만나기 전, 나는 다큐멘터리 영화 <프리 솔로>Free Solo를 봤다. 이 영화는 유명 등산가 알렉스 호놀드 Alex Honnold가 요세미티국립공원의 엘 캐피턴을 로프 없이 올라가는 과정을 기록한 것이다. 엘 캐피턴은 정상에 오르기까지 여덟 곳 정도의 고비가 있는데 이것은 수학으로 치면 리만 가설에 해당하는 구간이다. 그중 가장 어려운 고비에 해당하는 구간을 '볼더링 문제'라고 부른다. (196)
이 문장을 읽고 바로 유튜브에서 <프리 솔로> 장면을 봤다. 아무런 안전 장비도 없이 수직의 암벽을 오르는 모습은 보기만 해도 몸에 긴장감을 유발한다. 왜 이런 무모해 보이는 도전을 할까. 수학자가 난제를 풀어내는 것과 같은 희열을 알기 때문일 것이다.
제5장 다이어그램의 지름길
내가 가장 좋아하고 또 평소 이용하는 지도 중 하나는 런던의 지하철 노선도다. (...) 대신 1933년에 나온 해리 벡Harry Beck의 지하철 지도는 지하철역의 지리적 위치는 완전히 무시하고, 단지 철도 네트워크가 서로 어떻게 연결되었는가에 집중했다. 이 지도에 담긴 생각이 너무 혁명적이어서 처음에는 지하철 운영 회사로부터 사용을 거절당했다. (215)
지하철 노선도에도 역사가 있다는 사실을 알게 되었다. 1933년에 해리 벡이 거리보다는 연결성을 쉽게 이해할 수 있도록 만들었다. 대한민국은 일제 강점기 시대였으니 과학의 발전상이 많이 뒤처져 있었다.
이중 결합은 종종 단일 결합을 가진 분자에 비해 반응성이 더 높다. 오늘날 화학 분야에서는 이러한 다이어그램을 이용하여 화학 반응을 표현하는 데 너무 익숙해져 있다. (...) 지금도 다이어그램은 분자 세계 안에 숨어 있는 새로운 화학 구조를 발견하는 데 도움을 준다. (221)
때로는 숫자나 알파벳을 이용하는 것보다 다이어그램을 이용하면 한 눈에 의미를 쉽게 파악할 수 있다. 화학 결합을 보여주는 다이어그램도 대표적인 예다. 다이어그램을 표현하는 방식에도 각각의 의미가 있다. 이중 결합과 단일 결합의 차이는 반응성을 보여준다고 한다. 학창 시절보다 더 재미있게 화학이 다가오는 느낌이다.
내가 가장 좋아하는 책 중 하나는 앤드루 바이너Andrew Viner의 <음악을 위한 벤 다이어그램> Venn That Tune이다. 그는 로내 제목을 정할 때 벤 다이어그램을 이용했다. (232)
어떻게 벤 다이어그램으로 제목을 정하는지 궁금하다. 이 책은 다음에 읽어야 할 목록에 찜해두었다.
제6장 미적분의 지름길
미적분학의 핵심이 여기에 있다. 바로 미적분학이 0으로 나누는 것을 정당화하는 방법이다. (258)
'0'으로는 나눌 수 없다. 하지만 무한히 0에 가까운 수를 가정하고 나눌 수 있다. 미적분학이 이를 정당화해 주었다. 이것이 미적분학이 중요하고 인류의 발전에 기여한 부분이다.
자연 만물은 이런 방식으로 에너지가 가장 낮은 상태를 찾아낸다. 여기서 렌과 같은 건축가들은 최저 에너지 상태에 있는 현수선의 모양을 뒤집으면 자체적으로 무게를 지탱할 수 있는 돔 형태가 된다는 사실을 이용하였다. (260~261)
돔을 설계하는 방법이 현수선이 최저 에너지 상태로 처지는 것을 뒤집으면 된다는 점이 재미있게 다가온다.
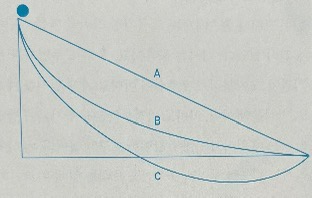
베르누이가 낸 문제는 가장 빠른 시간 안에 A 지점에서 B 지점까지 공을 굴러가게 하는 경사로를 설계하는 것이었다. 직선으로 경사로를 설계하는 것이 가장 빠르다고 생각할 수 있다. 혹은 공을 공중에 던졌을 때 그려지는 포물선을 거꾸로 뒤집어놓은 곡선을 떠올릴 수도 있다. 답은 둘 다 아니다. 가장 빠른 경로는 '사이클로이드' 형태인 것으로 밝혀졌다. 이 곡선은 움직이는 자전거 바퀴의 가장자리에 있는 한 점이 그리는 궤적에 해당하는 경로다. (265)
처음 위의 그림을 보았을 때 'A'가 아닐까 생각했다. 하지만 사이클로이드 형태로 구슬이 내려올 때 가장 빠르다. 새롭게 배운 유익한 정보다.
지침 예술instructional art이라는 아이디어가 새로운 것은 아니다. 이 아이디어는 마르셀 뒤샹이 1919년 여동생 수잔과 그의 신랑에게 자신이 주고 싶었던 결혼 선물을 직접 만들어보라는 안내서를 보낸 일화에서 유래했다. '행복하지 않은 기성품' Unhappy Ready-Made 이라는 이상한 이름이 붙은 결혼 선물을 동생 부부는 뒤샹을 대신해서 직접 만들어야 했다. (276)
지침 예술이란 용어가 생소하다. 예술가가 직접 만든 것이 아니라 누군가에게 안내서를 주고 타인이 안내에 따라 만든 작품이라고 할 수 있다. 1919년에 마르셀 뒤샹이 동생 부부에게 만들어보라고 한 것이 시초라니 역사에 놀라고 그 기발한 아이디어에 놀란다. 뒤샹은 이것이 하나의 작품이라고 생각하지 않았을 수도 있다. 후인들이 '지침 예술'이라 부른 것은 아닐는지. 이쪽 분야에 대한 지식이 부족해 좀 더 알아가야 할 부분이다.
'독서습관' 카테고리의 다른 글
| [993]에고라는 적_성공적인 인생을 위해 가져야할 마음 안내서 (1) | 2025.01.07 |
|---|---|
| [992]수학자의 생각법 ③_데이터와 확률 그리고 네트워크의 지름길 (0) | 2024.12.31 |
| [992]수학자의 생각법 ①_패턴 및 계산과 언어의 지름길을 찾아내는 기술 (0) | 2024.12.27 |
| [991]나는 빚을 다 갚았다_소비단식으로 직업의 자유를 얻기까지 (0) | 2024.12.26 |
| [990]카드모스와 하르모니아의 결혼_20세기 관점에서 보는 그리스 신화 (0) | 2024.12.23 |




댓글